Que peut-on découvrir avec deux informations ? |
- D’après ce qui précède (Phénomèbe binaire §2 ), avec une seule proposition A nous pouvons dire soit que A est vraie, soit que A est fausse (ou que
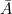 est vraie). Autrement dit, à une proposition correspondent deux possibilités.
est vraie). Autrement dit, à une proposition correspondent deux possibilités. - Avec deux propositions A, B, nous avons déjà défini deux nouvelles propositions (et, ou). D’où se pose la question : « Combien de propositions peut-on former avec deux propositions » ? Autrement dit, combien de circuits, logiques ou électriques, peut-on obtenir à l’aide de deux propositions initiales ?
Pour répondre à cette question il suffit de remplir, de toutes les façons possibles, les cases libres de la table de valeur ci-contre.
|
|
|||||||||||||||||||||||||||||
- Devrons-nous construire seize circuits logiques différents pour exprimer, à la sortie, ces seize «/nbsp;programmes » ? Non, car il est aisé de montrer que ces résultats s’expriment uniquement à l’aide des circuits « non », « et », « ou » (on peut même montrer qu’ils s’expriment avec deux seulement d’entre eux).Par exemple, d’après les résultats des paragraphes 2, 3, 4 :
- — La table I ci-dessous correspond à « non (A ou B) », soit
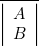 . En effet, par rapport à la table du paragraphe 4, les 0 sont remplacés par de 1 et inversement.
. En effet, par rapport à la table du paragraphe 4, les 0 sont remplacés par de 1 et inversement.
- — La table I ci-dessous correspond à « non (A ou B) », soit
— La table II ci-dessous correspond à « (non A) ou B », soit ![]() .
.
|
|
|||||||||||||||||||||||||||||||||||||
- — La table III ci-dessous correspond à « non (A et B) , soit

- En effet, par rapport à la table du paragraphe 3, les 0 et 1 ont été échangés.
A B 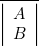
0 0 1 0 1 1 1 0 1 1 1 0 Table III A B ? 0 0 0 0 1 1 1 0 1 1 1 0 Table IV - — À quoi correspond la table IV ci-dessus ?
Les tables ci-dessous, construites de droite à gauche, montrent que la table IV correspond à
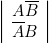 . Remarquons que cette table IV correspond au « ou exclusif » (en français : « soit…, soit…» ; de deux choses l’une, ou bien…ou bien). En effet, le résultat prend la valeur vraie (3
. Remarquons que cette table IV correspond au « ou exclusif » (en français : « soit…, soit…» ; de deux choses l’une, ou bien…ou bien). En effet, le résultat prend la valeur vraie (3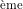 et 4
et 4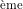 lignes) lorsque l’une des deux propositions A ou B est vraie à l’exclusion de l’autre.
lignes) lorsque l’une des deux propositions A ou B est vraie à l’exclusion de l’autre.
A B 0 0 0 1 1 0 1 1 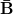
1 0 1 0 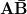
0 0 1 0 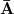
1 1 0 0 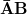
0 1 0 0 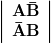
0 1 1 0 Un bon exercice consiste à procéder de même pour chacune des seize tables possibles.
- Interprétations ensemblistes.
- — Il est aisé d’interpréter, à l’aide des diagrammes de Venn ou de Carroll les seize propositions logiques obtenues à partir de deux propositions.
Ainsi, ci-dessous, nous avons représenté les ensembles correspondants aux tables I, II, III et IV ci-dessus.
Table I Table II A 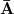
B 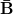
A 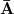
B 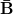
Table III Table IV A 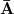
B 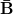
A 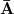
B 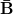
- — Un bon exercice consiste à illustrer ainsi les seize possibilités mises en évidence ci-dessus.
- — Il est aisé d’interpréter, à l’aide des diagrammes de Venn ou de Carroll les seize propositions logiques obtenues à partir de deux propositions.
Ainsi, ci-dessous, nous avons représenté les ensembles correspondants aux tables I, II, III et IV ci-dessus.
- Interprétations par montages électriques.
- — Rappelons que « et » est représenté par un montage en série (§3) et que « ou » est représenté par un montage en parallèle (§ 4).
- — Les montages ci-dessous « illustrent » les quatre tables de valeur ci-dessus. Nous laissons au lecteur le soin de procéder de même pour les autres tables.
Pour les montages I et III, il faut connaître les résultats suivants (démontrés au §6) :

- Interprétations par un mini-ordinateur.
- — Ces interprétations sont immédiates une fois que l’on sait que :
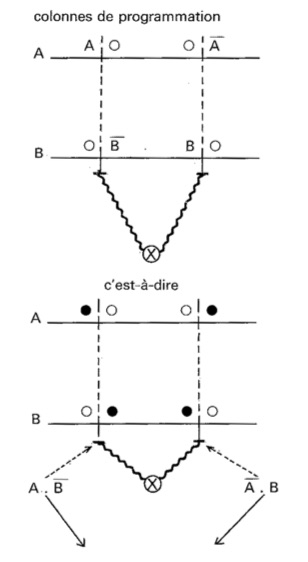
- à gauche (en regardant le pupitre de l’ordinateur J.R. 01) de chaque colonne de programmation (notée de 1 à 7), une fiche enfoncée dans un trou correspond, suivant la barrette A, B, C considérée, soit à A, soit à B, soit à C (rond plein) ;
- à droite de chaque colonne de programmation (dans les mêmes conditions), une fiche correspond soit à
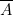 , soit à
, soit à 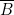 , soit à
, soit à 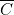 ;
; - deux colonnes de programmation reliées à la même lampe de sortie correspondent à « ou » ;
- pour « neutraliser » une proposition, on enfonce deux fiches de part et d’autre de la colonne de programmation.
- — Ainsi les quatre montages indiqués ci-dessus s’obtiendraient sur l’ Ordinateur J.R. 01, à l’aide des programmes I à IV ci-dessous, s’il n’y avait que deux barrettes A et B. En fait, la présence de la barrette C, qui permet une troisième information, modifie les schémas ci-dessous car il faut « neutraliser » (ne pas tenir compte de) cette troisième barrette. Nous étudierons ceci au paragraphe 7.
-
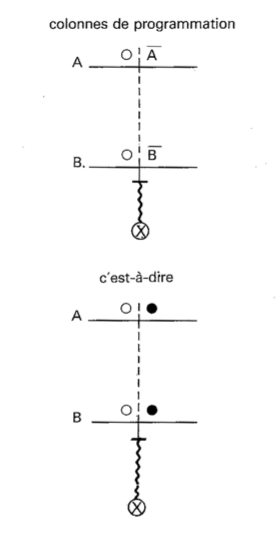
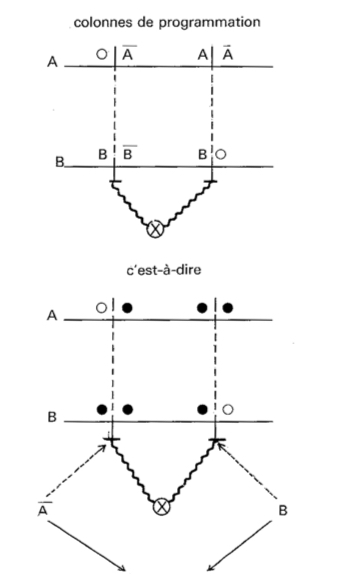
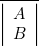
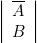

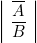
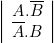
- — Ces interprétations sont immédiates une fois que l’on sait que :
